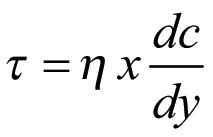Rörströmningsförluster
Rörströmningsförluster
Reynolds tal
Rörströmningsförluster eller strömningsförluster i rör, uppstår genom inverkan av inre friktion. Skjuvspänningar uppträder så snart en hastighetsgradient uppträder enligt följande
Ekv 11.12
där = dynamisk viskositet [Ns/m2]
c = strömningshastighet [m/s]
y = koordinat vinkelrätt strömningsriktningen [m]
Skjuvkrafternas arbete övergår i värme och ökar vätskans inre energi. Ökningen i inre energi medför att statiska trycket blir något mindre än det annars skulle ha blivit. Därav benämningen tryckförlust eller tryckfall.
Strömningsförlusterna är stora där skjuvspänningarna är stora dvs där hastighetsgradienterna är stora. Stora hastighetsgradienter förekommer i gränsskikt, vid strömning kring skarpa hörn, vid kraftiga virvelbindningar etc.
Vid rörströmning utbildas olika hastighetsfördelningar under olika förutsättningar. Som karakteristiskt tal vid friktionsbehäftad rörströmning använder man sig av Reynolds tal
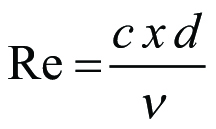
Ekv 11.13
Mellan den kinematiska viskositeten och den dynamiska viskositeten råder sambandet
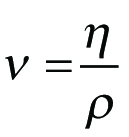
Ekv 11.14
där = vätskans densitet [kg/m3]
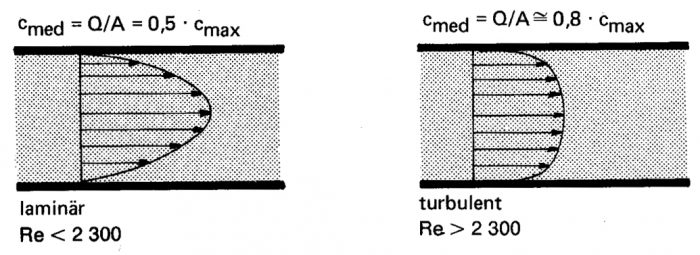
Vid låga Reynoldska tal (Re< 2300) är strömningen laminär och sker i skikt, som har olika hastigheter men som ej blandar sig med varande. Vid Re > 2300 är strömningen turbulent dvs vätskepartiklarna utför en oregelbunden rörelse överlagrad på huvudströmningen.
Figur 11.10 Laminär och turbulent strömning.
Eftersom hastighetsgradienterna är olika blir även skjuvspänningar och strömningsförluster olika i de båda fallen. Det kritiska Re-talet har angivits till Rekr = 2300. Man bör dock observera att strömningen kan vara laminär vid avsevärt högre Re-värden om strömningen är extremt väl skyddad från störningar. Låga värden på Reynolds tal uppträder vid små strömningshastigheter, vid liten rördiameter eller vid hög viskositet. För vatten av 20°C är = 1 · 10-6 m2/s. Omslag till turbulent strömning sker då vid
c · d = Rekr · ν =2300 · 10-6 = 2,3 · 10-3 [m2/s]
d = 1 m → c = 2,3 mm/s
d = 1 mm → c = 2,3 m/s
Av exemplet framgår att laminär strömning är mindre vanlig i tekniska sammanhang för vätskor med viskositet liknande vattens.
Strömningsförluster i rakrör
För strömningsförlusterna i ett rakrör gäller formeln
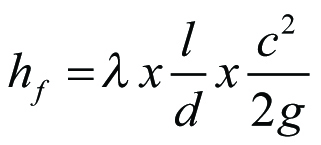
Ekv 11.15
där λ = förlustkoefficient för rakrör
l = rörlängd [m]
d = rördiameter [m]
c = Q/A = strömningshastighet [m/s]
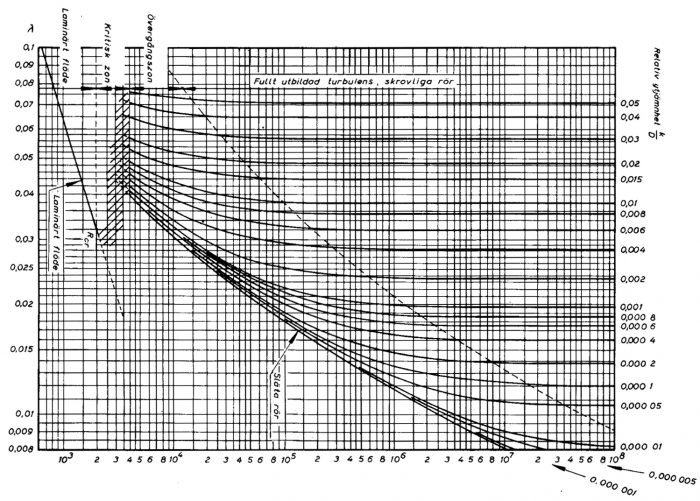
Förlustkoefficienten λ beror av Reynolds tal och av rörets skrovlighet och redovisas nedan i diagramform.
Figur 11.11 Förlustkoefficienten vid rakrör.
Förlustkoefficienten kan även beräknas ur följande formler:
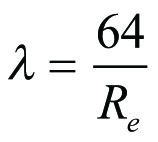
Ekv 11.16
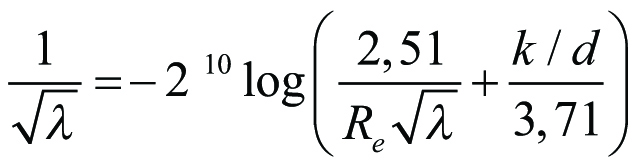
Ekv 11.17
Sambandet (11.17) kallas ibland Colebrook-Whites formel.
I området mellan Re = 2300 och Re = 4000 kan laminär och turbulent strömning omväxlande förekomma i olika delar av rörledningen. Den resulterande förlustkoefficienten antar då värden mellan de som ges av formlerna (11.16) och (11.17).
Uttrycket (11.17) är något obekvämt för handräkning. Inom det område i diagrammet (figur 11.11) där λ är oberoende av Re kan följande enklare formel användas:
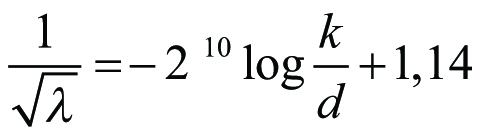
Ekv 11.18
Rörens skrovlighet kan bedömas med värden ur tabell 11.1.
Tabell 11.1 Exempel på ungefärlig skrovlighet för rör.
Andra i litteraturen ofta förekommande formler för beräkning av rakrörsförluster i det turbulenta området är de sk Hazen-Williams och Mannings formler. Dessa ger emellertid inga upplysningar utöver de tidigare presenterade sambanden, är icke dimensionsriktiga och utelämnas därför. Ytterligare diagram för beräkning av rakrörsförluster, se vidare avsnitt 11.4.
Engångsförluster
Strömningsförluster i böjar, ventiler etc kallas för engångsförluster och beräknas med hjälp av formeln Ekv 11.19
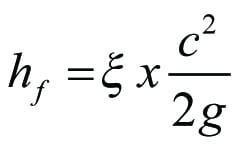
där ζ = förlustkoefficient vid engångdförluster
c = strömningshastighet [m/s]
Engångsförlusternas storlek påverkas liksom rakrörsförlusternas i princip av ytskrovlighet och Reynolds tal. Exempel på ungefärliga värden på förlustkoefficienten vid engångsförluster illustreras av tabell 11.2. Samtliga värden avser förhållanden vid normal ytskrovlighet och vid höga Reynoldska tal, dvs vid fullt utbildad turbulent strömning. I de fall där hastigheten förändras skall alltid den högsta strömningshastigheten användas vid beräkning av hf enligt ekv 11.19. Vid en areaförändring insättes den hastighet, som gäller vid den minsta diametern och vid T-rör den hastighet, som gäller för den sammanlagda volymströmmen.
Tabell 11.2 Ungefärliga värden för förlustkoefficienten vid engångförluster.
Ett alternativt sätt att uttrycka engångsförlusternas storlek är med hjälp av begreppet ekvivalent rörlängd lekv. Med lekv för exemplevis en rörböj menas den rakrörslängd, som ger upphov till samma tryckförlust som rörböjen vid lika strömningshastighet. Genom att sätta ekv (11.15) och ekv (11.19) lika erhålles
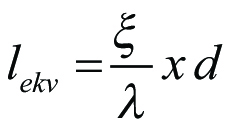
Ekv 11.20
Av ekv (11.20) framgår att ekvivalenta rörlängden är beroende av λ dvs rakrörets ytskrovlighet och Reynolds tal. Den är därför svår att ange som en specifik egenskap hos exempelvis en rörböj och får en överslagsmässig karaktär. För λ =0,02 blir för en rörböj 90° med kort radie (r=d) den ekvivalenta rörlängden lekv = 20 · d.
I avsnitt 11.4 anges vid grafisk rörberäkning användbara värden på ekvivalent rörlängd för vissa engångsförluster.
Hydraulisk diameter
Vid strömning i delvis fyllda cirkulära rör, i icke cirkulära rör eller i öppna kanaler kan strömningsförlusterna beräknas på principiellt samma sätt som beskrivits i tidigare avsnitt. I stället för det helt fyllda cirkulära rörets diameter måste emellertid i dessa fall den hydrauliska diametern dh införas.
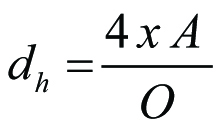
Ekv 11.21
där dh = hydraulisk diameter [m]
A = kanal vätskefyllda tvärsnittsarea [m2]
O = kanal vätskeberörda omkrets [m]
För ett helt fyllt cirkulärt rör blir dvs att i detta fall är hydraulisk och geometrisk diameter lika stora.
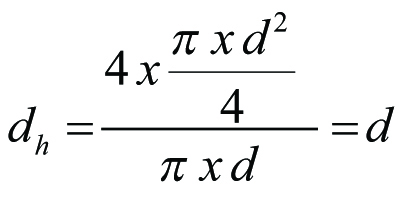
För ett till hälften fyllt cirkulärt rör blir
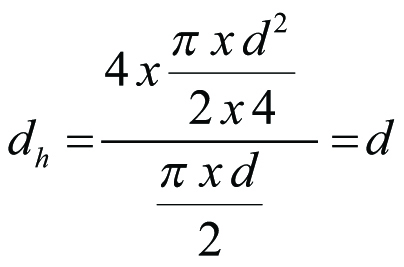
För en till hälften fylld rektangulär sektion blir
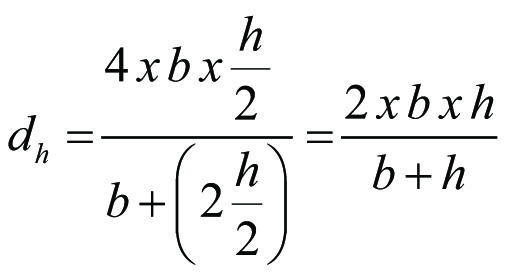
Med Reynolds tal
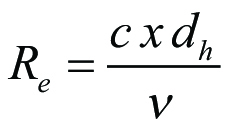
Ekv 11.22
och relativa skrovligheten k/dh gäller figur 11.11 och formlerna (11.16), (11.17) och (11.18) med oförändrade siffervärden.
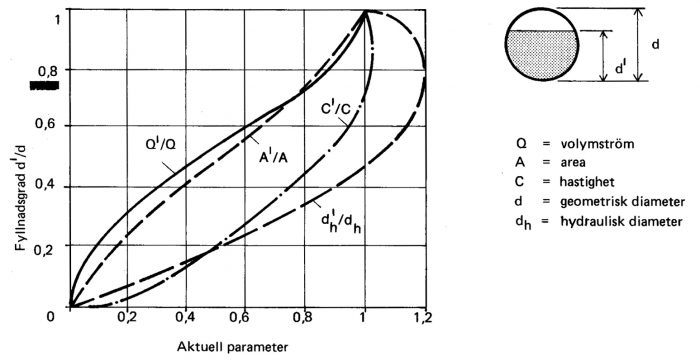
Vid ledningar med självfall kan röret arbeta delvis fyllt. Fyllnadsgraden beror bl a rörets lutning och driftsförhållanden. För ett cirkulärt rör definieras fyllnadsgraden av förhållandet dl/d där dl är vätskedjupet i röret och d rörets diameter. Figur 11.12 illustrerar hur olika strömningsparametrar varierar med fyllnadsgraden i röret. Såväl strömningshastigheten som hydrauliska diametern har sina största värden vid fyllnadsgrader strax under ett.
Figur 11.12 Strömning i delvis fyllt cirkulärt rör. (Primtecken = delvis fyllt, utan primtecken = helt fyllt).
Vid självfallsledningar med förorenade vätskor måste sedimenteringsrisken noga beaktas. Detta förhållande lägger vissa villkor på ledningens utformning och drift. Behandlingen av rörströmningsförluster under avsnitt 11.2 avser newtonska vätskor av vilka den vanligaste är vatten. De icke-newtonska vätskorna kräver speciell uppmärksamhet vid bestämning av uppträdande tryckförluster. För vidare studium hänvisas till avsnitt 11.4 friktionsförluster vid masspumpning samt till speciallitteraturen.
