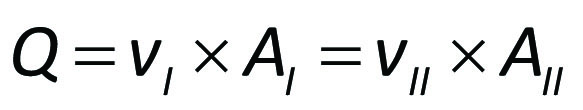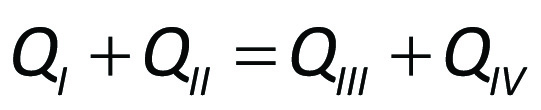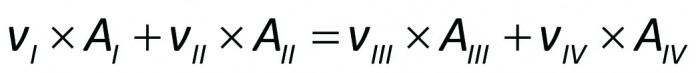- 1 Installation av pumpar
- 2 Skötsel och Underhåll av pumpar
- 3 Pumpar, funktion och konstruktion
- 3.1 Allmänt om Pumptyper
- 3.2 Rotordynamiska pumpars grunder
- 3.3 Förträngningspumpars grunder
- 3.4 Pumpkurvor
- 3.5 Pumpars sugförmåga, NPSH och kavitation
- 3.6 Centrifugalpumpars utföranden
- 3.6.1 Vattenpumpar
- 3.6.2 VVS pumpar
- 3.6.3 Vattenautomater
- 3.6.4 Länspumpar
- 3.6.5 Flerstegspumpar
- 3.6.6 Djupbrunnspumpar
- 3.6.8 Spolpumpar
- 3.6.9 Standardpumpar enligt ISO
- 3.6.10 Kemipumpar och processpumpar
- 3.6.11 Tätningslösa pumpar
- 3.6.12 Pumpar av plast
- 3.6.13 Massapumpar
- 3.6.14 Godspumpar
- 3.6.15 Livsmedelspumpar
- 3.6.16 Stockningsfria pumpar
- 3.6.17 Dubbelsidigt sugande pumpar
- 3.6.18 Propellerpumpar
- 3.7 Vätskeringpumpar
- 3.8 Förträngningspumpars utförande
- 3.9 Övriga pumpar
- 3.11 Pumpval
- 4 Material och materialval
- 4.1 Inledning
- 4.2 Materialöversikt för pumpar
- 4.3 Materialhållfasthet och trycktäthet för pumpar
- 4.4 Korrosion och Erosion på pumpar
- 4.5 Materialval pumpar för slitande vätskor
- 4.6 Kavitationsbeständiga material i pumpar
- 4.7 Materialkombinationer och materialval i pumpar
- 4.8 Praktiska problemställningar vid materialval för pumpar
- 5 Pumptätningar
- 6 Axelkopplingar för pumpar
- 6.2 Val av axelkoppling
- 6.3 Typ av koppling för pumpar
- 6.4 Uppriktningsfel för pumpar
- 6.5 Axelkopplingar, krafter och moment
- 6.6 Pumpkopplingar och dess driftsfaktorer
- 6.7 Pumpkopplingars varvtal, dimensioner och vikt
- 6.10 Pumpkopplingar, uppställning och demontering
- 6.11 Pumpkopplingars livslängd och kostnader
- 6.12 Pumpaxlars uppriktning
- 7 Drivutrustning för pumpar
- 8 Flödesreglering för pumpar
- 8.2 Anpassning av pumphjulets diameter
- 8.3 Seriekoppling och parallellkoppling av pumpar
- 8.4 Polomkopplingsbar asynkronmotor
- 8.5 Start och stoppreglering av pumpar
- 8.6 Driftsföljder vid start- stoppreglering
- 8.7 Magasinsvolymer vid start-stopp reglering
- 8.8 Kontinuerlig reglering av pumpar
- 8.9 Strypreglering av pumpar
- 8.10 Shuntreglering av pumpar
- 8.11 Varvtalsreglering av pumpar
- 8.12 Ekonomiska aspekter vid varvtalsreglering av pumpar
- 8.13 Val av utrustning för varvtalsreglering av pumpar
- 9 Storheter och enheter för pumpar
- 10 Vätskors egenskaper
- 11 Vätskeströmning
-
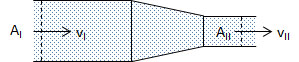
11.1.1 Kontinuitetsekvationen
Kontinuitetsekvationen är ett uttryck för villkoret att massa varken skapas eller försvinner vid ett strömningsförlopp
Förutsättes att strömningen är stationär, måste massflödet ṁ vara lika stort överallt längs röret eller strömröret. För det endimensionella fallet i figur 11.2 blir
eller för en inkompressibel vätskeströmning
-
Där
Q = volymström [m³/s]
v = Q/A = strömningshastighet [m/s]
A = tvärsnittsarea [m²]När tvärsnitten i ett rör minskar, ökar således strömningshastigheten enligt kontinuitetsekvationen (11.2). Halveras arean, fördubblas hastigheten o s v.
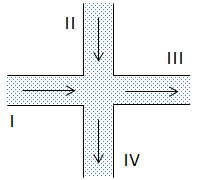
Eftersom ingen ansamling av massa sker vid förgreningen, måste lika mycket massa per tidsenhet strömma ut som in. Med beteckningar enligt figur 11.3 blir
eller
-
Kontinuitetsekvationen exempel
Kirchhoffs första lag beskriver hur strömmar förgrenar sig i en krets, ”När ström flyter in i en ände av en ledare flödar den genast ut i andra änden av ledaren”. Det finns många likheter i beskrivningen av flöden i rörledningar och lagar för elektriska ledare. Kirchhoffs lagar kan därför användas för att förstå och appliceras med framgång för att lösa ut flöden och tryckfall i ett rörsystem med stabilt flöde i balans.
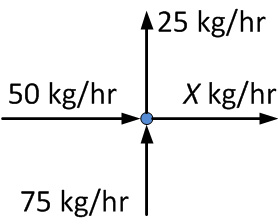
Med flöden enligt figur 11.3c kan vi använda Kirchhoffs första lag och upprätta en ekvation där vi löser ut flödet X i kretsen.
(-50)+(-75)+(25)+(X)=0
X =100 kg/hr
Vill du lära dig mer om beräkning av flöden i pumpsystem rekommenderar vi kursen Piping System Fundamentals >>>