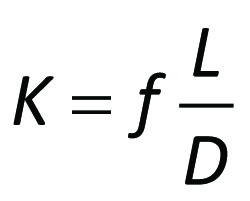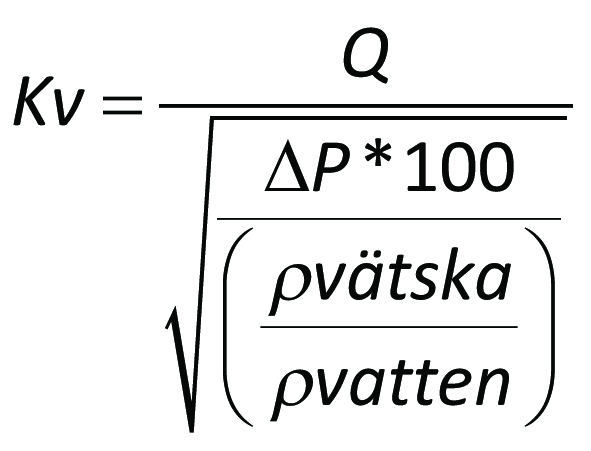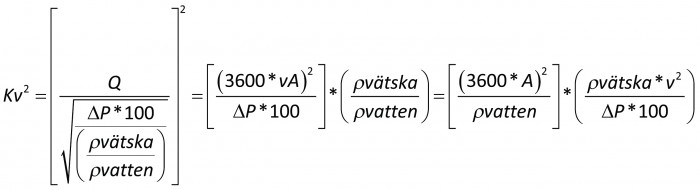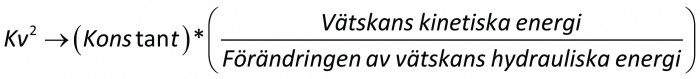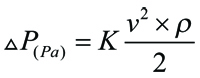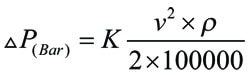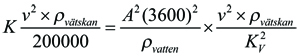Relationen mellan flödeskoefficient Kv och motståndskoefficient K
Vad är relationen mellan flödeskoefficienten Kv och motståndskoefficienten K, som båda används för beräkning och dimensionering av ventiler, rörkrökar och andra komponenter i pumpsystem.
En komponent med ett flöde genom sig har en specifikation som anger hur den påverkar systemet vid olika flöden. Tillverkare av reglerventiler anger detta i flödeskoefficienten Kv (även Cv som är den amerikanska flödeskoefficienten, se förklaring nedan) som visar flödet genom reglerventilen vid tryckfallet 1 bar. Andra komponenter som avstängningsventiler, backventiler, T-rör och rörkrökar är definierade genom en enhetslös motståndskoefficient K som speglar motståndet komponenten utgör i systemet.
Dimensionering av pumpsystem
För att dimensionering och drift av pumpsystem i olika typer av applikationer ska bli så kostnadseffektiv som möjligt är noggrannheten vid beräkning en kritisk faktor. I princip uppför sig pumpar och ventiler likadant oavsett om vi pratar om processindustrier, VA-anläggningar eller fastigheter även om det självklart finns olika faktorer att ta hänsyn till inom de olika segmenten. För dimensionering i allmänhet gäller dock att om man underdimensionerar så räcker inte kapaciteten till och därför tenderar vi att överdimensionera systemen för att eliminera den risken.
När vi överdimensionerar betalar vi mer för anläggningen än vad vi i själva verket behöver, stor pump kostar mer än liten pump, vilket leder till högre investeringskostnader, driftskostnader och underhållskostnader. Överdimensionering är alltså något som kostar oss en stor påse pengar vilket de flesta är medvetna om, men i tillägg till den medvetna överdimensioneringen, bidrar även (o)säkerhetsfaktor och felaktiga beräkningar till överdimensionerade system. Felaktiga beräkningar är ofta den mänskliga faktorns fel och ibland stöter vi på exempel där det är uppenbart att den som beräknat systemet haft för många bollar i luften samtidigt.
Ett vanligt fel är att blanda ihop enheter, formler och koefficienter. Två av de vanligare förekommande koefficienterna är Kv och K och att blanda ihop dessa kan leda till misstag som blir kostsamma att rätta till i efterhand.
De två koefficienterna är alltså omvänt relaterade i det att flödeskoefficienten Kv representerar hur stor flödeskapacitet hindret (reglerventilen) tillåter vid ett känt tryckfall medan motståndskoefficienten ger oss motståndet som hindret (rörkröken) utgör vid ett visst flöde.
Båda uttrycken följer energiprincipen, lagen om energins bevarande, för strömmande vätska genom ett hinder. Vi börjar med att förklara motståndskoefficienten.
Motståndskoefficienten K
Motståndskoefficienten K är ett dimensionslöst värde som alltså talar om för oss, hur stort motstånd den aktuella komponenten ger vid ett vist flöde. Vi kan beräkna K genom att sätta in värden på respektive känd faktor i formeln:
(Ekv.1)
där
f = Darcys friktionsfaktor
L= rörlängd i meter
D= rördiameter i mm
L/D = Ekvivalent rörlängd (enhetslös)
Vill ni veta med om hur man räknar på pumpsystem, rekommenderar vi kursen Piping System Fundamentals >>>
Motståndskoefficienten, K kan också användas för att räkna ut tryckfall, alltså hur stor förlust en komponent utgör i systemet. Förlusten för enskilda komponenter kan beräknas antingen i tryckfall (bar eller Pascal) eller höjdförlust i meter vätskepelare (mvp). Formeln för att beräkna komponenters höjdförlust (hf) i mvp är en variant av Darcys formel för beräkning av förluster i rörledningar och beräknas genom formeln:
(Ekv.2) hf = K ( v²/2g ) , där
hf = energiförlusten (höjdförlust) i meter vätskepelare (mvp) som uppstår genom friktion, här uttryckt i meter
v = vätskans genomsnittliga flödeshastighet i m/s
g = tyngdaccelerationen 9,81 m/s²
Energiförlusten i meter (mvp) är också relaterad till tryckfallet, differenstrycket ΔP (bar), genom komponenten med hänsyn till vätskans densitet ρ – rå (kg/m³) genom formeln:
(Ekv.3) hf = (100*ΔP)/(ρ g)
Genom att lösa ut K i ekvation 2 och sätta in resultatet i ekvation 3 får vi:
(Ekv.4) K = (2g/v²) * hf = 2g * 100 ΔP / ρv²
2g är en konstant alltså är K
Flödeskoefficienten Kv
I sin enklaste form kan flödeskoefficienten skrivas som
där
Q = flödet i m³/h
ΔP = differenstrycket (Pin-Put) i bar
ρvätska = pumpad vätskans densitet (kg/m³)
ρvatten ≅ 1000 kg/m³
Flödeskoefficienten Kv representeras alltså av enheten m³/h /√ΔP (flödet i m³/h genom kvadraten ur ΔP). Det gör det lite svårare att åskådliggöra relationen till motståndskoefficienten K men om vi börjar med att definiera de olika beståndsdelarna och härleder formlerna får vi svaret.
Det volymetriska flödet Q i m³/h räknas ut ifrån den genomsnittliga flödeshastigheten genom ett tvärsnitt.
(Ekv.6) q (m³/s) = v (m/s) * A (m²)
eller
(Ekv.6.1) Q (m³/h) = 3600 * v (m/s) * A (m²) = 3600 v * A (m³/h)
där
A = ett tvärsnitt av rördiametern
Om vi likställer båda sidor av ekvation 5 och ersätter Q med ekvation 6.1 får vi:
Ekvation 7
Eftersom vattnets densitet (≅ 1000) är konstant och arean också är en konstant för vårt system, kan vi förenkla ekvation 7, kvadraten av Kv är alltså:
Relationen mellan Kv och K
När vi nu har klart för oss vad Kv och K egentligen uttrycker ska vi härleda och bestämma relationen mellan de båda. Ekvation 4 och 7 kan vi omvandla för att lösa ut differenstrycket ΔP. När det är gjort kan vi likställa dessa ekvationer:
Vi löser ut ΔP i ekvation 4:
För att sedan översättas tryckfall (bar) genom ekvationen:
Löser vi ut ΔP i ekvation 7 får vi:
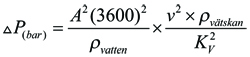
Ekv.10
Nu har vi två ekvationer som är ger ΔP, i den ena har vi K i den andra Kv, sätter vi högerled i ekvation 9 och 10 på var sida så likställer vi dessa ekvationer.
Flödeshastigheten v² och densiteten för vätskan (ρvätskan) tar ut varandra. Densiteten för vatten sätter vi till 1000, en förenkling som gäller vid 4 grader men som hjälper oss att lösa alla kända till en konstant 0,04. Vi känner nu alla faktorer utom K, Kv och genomlopps diametern d som varierar i ett pumpsystem. Löser vi nu ut exempelvis Kv ur ekvationerna får vi:
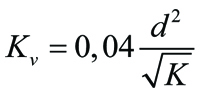
Där är sambandet, relationen och skillnaden mellan flödeskoefficienten Kv och motståndskoefficienten K.
Vill ni veta mer om detta eller något annat om pumpar och pumpsystem är ni välkomna att kontakta Pumpportalen!